|
 |
| J Korean Acad Pediatr Dent > Volume 45(1); 2018 > Article |
|
ņ┤łļĪØ
ļ│Ė ņŚ░ĻĄ¼ņØś ļ¬®Ēæ£ļŖö ņĖĪļ░® ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ņé¼ņ¦äņØś ļČäņäØņŚÉ ņØ┤ņÜ®ļÉśļŖö ņåīĒöäĒŖĖņø©ņ¢┤ņØś ņåīĻĖēņä▒ ĒÖĢļ│┤ņÖĆ ņĖĪņĀĢĻ░ÆņØś ļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśļŖö Ļ▓āņØ┤ļŗż. ļśÉĒĢ£ ņØ┤ļź╝ ņØ┤ņÜ®ĒĢ┤ ņåīņĢäņŚÉņä£ ĻĄÉņĀĢņ╣śļŻīļź╝ ņ£äĒĢ£ Ļ│äņĖĪĻ░ÆņØś ņ░ĖĻ│Ā Ēæ£ņżĆņØä ņ¢╗ĻĖ░ ņ£äĒĢ£ ĻĖ░ļ░śņØä ļ¦łļĀ©ĒĢśĻ│Āņ×É ĒĢśņśĆļŗż.
ĻĄÉņĀĢņ╣śļŻīļź╝ ņ£äĒĢ┤ ņä£ņÜĖļīĆĒĢÖĻĄÉ ņ╣śĻ│╝ļ│æņøÉ ņåīņĢäņ╣śĻ│╝ņŚÉ ļé┤ņøÉĒĢ£ 6ņäĖņŚÉņä£ 13ņäĖ ņé¼ņØ┤ ĒÖśņĢä ņżæ 1ĻĖē ļČĆņĀĢĻĄÉĒĢ®ņ£╝ļĪ£ ņ¦äļŗ© ļ░øņØĆ ĒÖśņĢä 100ļ¬ģņØś ļŹ░ņØ┤Ēä░ļź╝ ņłśņ¦æĒĢśņśĆļŗż. ņåīĻĖēņä▒ ĒÖĢļ│┤ļź╝ ņ£äĒĢ┤ ļ░®ņé¼ņäĀ ņ┤¼ņśüņØ┤ Ļ░ĆļŖźĒĢ£ phantom ņןļ╣äļź╝ ņĀ£ņ×æĒĢśņśĆņ£╝ļ®░, Ēśäņ×¼ ņé¼ņÜ®ņżæņØĖ Ļ│äņĖĪ ņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ phantom ņןļ╣äņØś ĻĖĖņØ┤ņÖĆ Ļ░üļÅäļź╝ ņĖĪņĀĢĒĢśņŚ¼ ņåīĒöäĒŖĖņø©ņ¢┤ņØś ĻĄÉņĀĢĻ░ÆņØä Ļ│äņé░ĒĢśņśĆļŗż. ļČłĒÖĢļÅä Ļ│äņé░ņØä ņ£äĒĢ┤ 100ļ¬ģņØś ņĖĪļ░®ļæÉļČĆļ░®ņé¼ņäĀ ņśüņāü Ļ│äņĖĪĻ░ÆĻ│╝ ļ░śļ│ĄņĖĪņĀĢņŚÉ ņØśĒĢ£ ļČłĒÖĢļÅäņÖĆ(AĒśĢ ļČłĒÖĢļÅä) ņĄ£ņåīļČäĒĢ┤ļŖźĻ│╝ ļæÉļČĆņØś ņ£äņ╣śņŚÉ ņØśĒĢ£ ļČłĒÖĢļÅäļź╝(BĒśĢ ļČłĒÖĢļÅä) Ļ│äņé░ĒĢśņśĆļŗż. ņØ┤ļź╝ ĒåĄĒĢ┤ ĒĢ®ņä▒Ēæ£ņżĆļČłĒÖĢļÅäļź╝ ņ¢╗ņŚłņ£╝ļ®░ ņĄ£ņóģņĀüņ£╝ļĪ£ ĒÖĢņןļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśņśĆļŗż.
ļ│Ė ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ Ēśäņ×¼ ņé¼ņÜ®ņżæņØĖ ņĖĪļ░®ļæÉļČĆļ░®ņé¼ņäĀņé¼ņ¦ä Ļ│äņĖĪ ĒöäļĪ£ĻĘĖļשņØ┤ ļåÆņØĆ ņĀĢĒÖĢņä▒Ļ│╝ ņŗĀļó░ļÅäļź╝ Ļ░Ćņ¦ĆļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļśÉĒĢ£ ĻĄÉņĀĢĻ░ÆņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņĖĪĻ░ÆņØä ĻĄÉņĀĢĒĢśņśĆņ£╝ļ®░, 6 - 13ņäĖ ĒĢ£ĻĄŁņØĖ ņåīņĢäņŚÉņä£ņØś ĻĄÉņĀĢĻ│äņĖĪņ╣śņØś ļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśņŚ¼ 1ĻĖē ļČĆņĀĢĻĄÉĒĢ® ĒÖśņĢäņØś ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś 95% ņŗĀļó░ļÅäļź╝ Ļ░Ćņ¦ĆļŖö ļČäĒżļ▓öņ£äļź╝ ņĀ£ņŗ£ĒĢśņśĆļŗż.
Abstract
The aim of this study was to obtain the traceability of the software used to analyze lateral cephalometry and to calculate the uncertainty of the measurements. Furthermore, this study aimed to provide a basis for obtaining standard references for measurement values for orthodontic treatment in children.
Cephalometric data were collected from 100 children diagnosed with class I malocclusion between the ages 6 to 13 years who visited the pediatric dentist at Seoul National University Dental Hospital. To ensure traceability, a phantom device was created. Correction values were calculated by measuring the length and angle of the phantom device using the software. Type A uncertainty was calculated by obtaining the standard deviation of cephalometric measurements of 100 persons and the standard error of repeated measurements. Determination of the type B uncertainty was induced by minimum resolution and the position of the head. Using these, the combined standard uncertainty was obtained and the expanded uncertainty was calculated.
The results of this study confirm that the currently used software has high accuracy and reliability. Furthermore, the uncertainty of orthodontic measurements in Korean children aged 6 to 13 years was calculated, and distribution range for class I malocclusion with 95% confidence interval was suggested.
ļ¼╝ļ”¼ļ¤ēņŚÉ ļīĆĒĢ£ ņĖĪņĀĢ Ļ▓░Ļ│╝ļź╝ ļ│┤Ļ│ĀĒĢĀ ļĢīļŖö ĻĘĖ Ļ░ÆņØś ņŗĀļó░ļÅäļź╝ ļéśĒāĆļé┤ļŖö ņ¢┤ļ¢ż ņĀĢļ¤ēņĀüņØĖ Ļ░ÆņØä ĒĢ©Ļ╗ś ļéśĒāĆļé┤ņ¢┤ņĢ╝ ĒĢ£ļŗż. ņØ┤ļź╝ ĒåĄĒĢ┤ ņĖĪņĀĢ Ļ▓░Ļ│╝ļź╝ ņØ┤ņÜ®ĒĢśļŖö ņé¼ļ×īļōżņØ┤ ĻĘĖ Ļ▓░Ļ│╝ņØś ņŗĀļó░ļÅäļź╝ ĒÅēĻ░Ć ĒĢĀ ņłś ņ׳Ļ│Ā, ļŗżļźĖ ņĖĪņĀĢ Ļ▓░Ļ│╝ļéś Ēæ£ņżĆĻ│╝ ļ╣äĻĄÉ ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ ĻĘ╝ļלņŚÉļŖö ļČłĒÖĢļÅäņØś Ļ░£ļģÉņØ┤ ļÅäņ×ģļÉśņ¢┤ ļäÉļ”¼ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŗż[1,2]. ļČłĒÖĢļÅä(Uncertainty)ļŖö ŌĆ£ņĖĪņĀĢļ¤ē Ļ░ÆņØä ĒĢ®ļ”¼ņĀüņ£╝ļĪ£ ņČöņĀĢĒĢ£ Ļ░ÆļōżņØś ļČäņé░ĒŖ╣ņä▒ņØä ļéśĒāĆļé┤ļŖö ĒīīļØ╝ļ»ĖĒä░ŌĆØļĪ£ ņĀĢņØśļÉśļ®░ ņĖĪņĀĢļ¤ēņØś ņĄ£ņäĀņØś ņČöņĀĢĻ░Æļ┐Éļ¦ī ņĢäļŗłļØ╝ ņČöņĀĢĻ░Æ ļ▓öņ£äņØś ņŗĀļó░ ņĀĢļÅäļź╝ ņØśļ»ĖĒĢ£ļŗż[1]. ņ”ē, ņĖĪņĀĢĻ▓░Ļ│╝ņØś ļČłĒÖĢļÅäļ×Ć ņŚ¼ļ¤¼ ļ▓ł ņĖĪņĀĢņØä ĒĢśņśĆņØä ļĢī ņĖĪņĀĢĻ░ÆņØ┤ ļČäĒżĒĢśļŖö ļ▓öņ£äļź╝ ņ¢┤ļŖÉ ņĀĢļÅä ņŗĀļó░ĒĢĀ ņłś ņ׳ļŖöņ¦ĆņŚÉ ļīĆĒĢ£ Ļ░£ļģÉņØ┤ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ░£ļģÉņØĆ ĒÖöĒĢÖ, ņāØĒÖöĒĢÖ, ņāØļ¼╝ĒĢÖ, ņ×äņāü ņāØļ¼╝ĒĢÖ, ņĢĮļ”¼ĒĢÖ, ļ▓ĢņØśĒĢÖ, ļÅģņä▒ĒĢÖ, ĒÖśĻ▓Į, ļåŹņŚģ ļ░Å ņŗØĒÆł ļČäņäØĻ│╝ Ļ░ÖņØ┤ ļČäņäØ Ļ▓░Ļ│╝ļź╝ ņĀĢļ¤ēĒÖö ņŗ£ĒéżļŖö ļČäņĢ╝ņŚÉņä£ ņżæņÜöĒĢśĻ▓ī Ļ│ĀļĀżļÉśņ¢┤ņĢ╝ ĒĢ£ļŗż[3]. ņØśĒĢÖ ļČäņĢ╝ņŚÉņä£ļÅä ņāØļ”¼ĒĢÖņĀü, ņāØĒÖöĒĢÖņĀü ļ│Ćņłś ļō▒ņØä ņĖĪņĀĢĒĢ£ Ļ▓░Ļ│╝Ļ░Ć ņ×äņāüņĀüņ£╝ļĪ£ ņ¦äļŗ©ņØ┤ļéś ņ╣śļŻīĻ│äĒÜŹ ņłśļ”ĮņŚÉ ņØ┤ņÜ®ļÉśĻ│Ā ņ׳ļŗż. ņĖĪņĀĢ ļŗ©Ļ│äņŚÉņä£ ņĀĢļ¤ēĒÖöĻ░Ć ņלļ¬╗ļÉśļŖö Ļ▓ĮņÜ░ ņ¦łļ│æņØś ņ¦äļŗ©ņØä ņ£äĒĢ£ ņØśņé¼ Ļ▓░ņĀĢņŚÉ ņśüĒ¢źņØä ļ»Ėņ╣śĻ│Ā, ĒĢ┤ļŗ╣ ļ│ĆņłśņØś ņ╣śļŻī ļ¬®Ēæ£ ņĪ░ņĀłņØ┤ ņ¢┤ļĀĄĻ▓ī ļÉ£ļŗż. ņĄ£ĻĘ╝ ĻĖ░ņłĀņØś ļ░£ļŗ¼ļĪ£ ņ¦äļŗ© ļ░Å ņ╣śļŻīņŚÉ ņé¼ņÜ®ļÉśļŖö ņØśļŻī ĻĖ░ĻĖ░ņØś ņłśĻ░Ć ņ”ØĻ░ĆĒĢśĻ│Ā ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ ņĀĢĒÖĢĒĢ£ ņĖĪņĀĢņØĆ ĒĢäņłśņĀüņØ┤ļŗż[4].
ņ╣śņØśĒĢÖņŚÉņä£ļÅä ņĖĪņĀĢņØä ĒåĄĒĢ┤ ņ¢╗ņØĆ ņĀĢļ¤ēņĀü ņĀĢļ│┤ļź╝ ņØ┤ņÜ®ĒĢ£ ņ¦äļŗ© ļ░Å ņ╣śļŻīĻ░Ć ņØ┤ļŻ©ņ¢┤ņ¦ĆĻ│Ā ņ׳ļŗż. ĻĘĖ ņżæ ĒĢśļéśņØĖ ņĖĪļ░®ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņśüņāü ļČäņäØņØĆ 1931ļģä Broadbent[5]ņŚÉ ņØśĒĢ┤ ļÅäņ×ģļÉ£ ņØ┤Ēøä ļČĆņĀĢĻĄÉĒĢ®ņØś ņ¦äļŗ©, ņ╣śļŻīĻ│äĒÜŹ ņłśļ”Į, ņä▒ņןĻ│╝ ņ╣śļŻī Ļ▓░Ļ│╝ ļō▒ņØä ļČäņäØĒĢśĻĖ░ ņ£äĒĢ£ ļÅäĻĄ¼ļĪ£ ņé¼ņÜ®ļÉśņ¢┤ ņÖöļŗż. ļ¦ÄņØĆ ņŚ░ĻĄ¼ņ×ÉņŚÉ ņØśĒĢ┤ ņ╣śņĢäņÖĆ ņ╣śņĢä, ņ╣śņĢäņÖĆ ņĢģņĢłļ®┤, ņĢģņĢłļ®┤Ļ│╝ ļæÉĻ░£ņĀĆ, ņĢģĻ░ä Ļ┤ĆĻ│äļź╝ ļČäņäØĒĢśĻĖ░ ņ£äĒĢ£ Ļ│äņĖĪņĀÉĻ│╝ ĻĖ░ņżĆ ĒÅēļ®┤ņØ┤ ņĀ£ņĢłļÉśņŚłļŗż[6]. Ēśäņ×¼ņŚÉļŖö ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦ä ļČäņäØ ņŗ£ ņłśļÅÖņĀüņØĖ ļ░®ļ▓ĢĻ│╝ ņ╗┤Ēō©Ēä░ļź╝ ņØ┤ņÜ®ĒĢśļŖö ļ░®ļ▓Ģ ļæÉ Ļ░Ćņ¦Ćļź╝ ņé¼ņÜ®ĒĢśĻ│Ā ņ׳ļŗż[7]. ņĄ£ĻĘ╝ņŚÉļŖö ļööņ¦ĆĒäĖņśüņāüņØś ļ░£ņĀäņ£╝ļĪ£ ņØĖĒĢ┤ ņ╗┤Ēō©Ēä░ļź╝ ņØ┤ņÜ®ĒĢ£ ļČäņäØņØ┤ ļ¦ÄņØ┤ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ņ£╝ļ®░, ņØ┤ļź╝ ņ£äĒĢ┤ ļ¦ÄņØĆ ļČäņäØĒöäļĪ£ĻĘĖļשņØ┤ ņāüņÜ®ĒÖö ļÉśņ¢┤ ņ׳ļŗż[8-13].
ĒĢśņ¦Ćļ¦ī ņØ┤ļ¤¼ĒĢ£ ļČäņäØĒöäļĪ£ĻĘĖļשņØä ĒåĄĒĢ┤ Ļ│äņé░ļÉ£ Ļ│äņĖĪĻ░ÆņØś ņĀĢĒÖĢļÅäļź╝ ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ņåīĻĖēņä▒ņØä ĒÖĢļ│┤ĒĢ£ ņāüĒā£ļĪ£, ļČłĒÖĢļÅäļź╝ Ļ│ĀļĀżĒĢśņŚ¼ Ļ│äņĖĪņ╣śļź╝ Ļ│äņé░ĒĢ£ ņŚ░ĻĄ¼ļŖö Ļ▒░ņØś ņĀäļ¼┤ĒĢśļŗż. ņåīĻĖēņä▒(Traceability)ņØ┤ļ×Ć ŌĆ£ļ¬©ļōĀ ļČłĒÖĢļÅäĻ░Ć ļ¬ģĒÖĢĒ׳ ĻĖ░ņłĀļÉśĻ│Ā ļüŖņ¢┤ņ¦Ćņ¦Ć ņĢŖļŖö ļ╣äĻĄÉņØś ņŚ░Ļ▓░Ļ│Āļ”¼ļź╝ ĒåĄĒĢśņŚ¼, ļ¬ģĒÖĢĒĢ£ ĻĖ░ņżĆ(ĻĄŁĻ░Ć ļśÉļŖö ĻĄŁņĀ£Ēæ£ņżĆ)ņŚÉ ņŚ░Ļ┤Ćņŗ£Ēé¼ ņłś ņ׳ļŖö Ēæ£ņżĆ Ļ░ÆņØ┤ļéś ņĖĪņĀĢĻ▓░Ļ│╝ņØś ĒŖ╣ņä▒ŌĆØņ£╝ļĪ£ ņĀĢņØśļÉ£ļŗż[1]. ņĖĪņĀĢņןļ╣äņØś ņĀĢĒÖĢņä▒ņØä ņ£äĒĢ┤ņä£ļŖö ļŹö ļåÆņØĆ ņĀĢĒÖĢļÅäļź╝ Ļ░Ćņ¦ä ņĖĪņĀĢņןļ╣ä, ņØ╝ņ░© Ēæ£ņżĆĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ ņĖĪņĀĢņØś ņĀĢĒÖĢņä▒ņØä ĒÖĢņØĖ ļ░øļŖö Ļ▓āņØ┤ ĒĢäņłśņĀüņØ┤ļŗż. ņ”ē, ņåīĻĖēņä▒ņØ┤ ĒÖĢļ│┤ļÉśņ¦Ć ņĢŖņØĆ ņןļ╣ä Ēś╣ņØĆ ņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ĒåĄĒĢ┤ Ļ│äņé░ļÉśļŖö ņĖĪņĀĢĻ░ÆņØĆ ĻĘĖ Ļ░ÆņØ┤ ņŗżņĀ£Ļ░ÆņØä ļ░śņśüĒĢśļŖö ņĀĢĒÖĢĒĢ£ Ļ░ÆņØĖņ¦Ć ĒÖĢņØĖĒĢśļŖö Ļ▓āņØ┤ ļČłĻ░ĆļŖźĒĢśļŗż. ĒĢśņ¦Ćļ¦ī Ēśäņ×¼ ņ╣śņØśĒĢÖļČäņĢ╝ņŚÉņä£ ņé¼ņÜ®ļÉśļŖö ņ╣śĻ│╝ņĖĪņĀĢņןļ╣ä ļ░Å ļČäņäØņåīĒöäĒŖĖņø©ņ¢┤ņØś Ļ▓ĮņÜ░ ļīĆļČĆļČä ņåīĻĖēņä▒ņØ┤ ĒÖĢļ│┤ļÉśņ¦Ć ņĢŖņØĆ ņ▒äļĪ£ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĖĪļ░®ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦äņØś ļČäņäØņŚÉ ņØ┤ņÜ®ļÉśļŖö ņåīĒöäĒŖĖņø©ņ¢┤ņØś ņåīĻĖēņä▒ņØä ĒÖĢļ│┤ĒĢśĻ│Ā Ļ│äņĖĪņ╣śņØś ļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśĻ│Āņ×É ĒĢśņśĆļŗż. ļśÉĒĢ£ ņØ┤ļź╝ ņØ┤ņÜ®ĒĢ┤ ņåīņĢäņŚÉņä£ ĻĄÉņĀĢņ╣śļŻīļź╝ ņ£äĒĢ£ Ļ│äņĖĪĻ░ÆņØś ņ░ĖņĪ░Ēæ£ņżĆņØä ņ¢╗ĻĖ░ ņ£äĒĢ£ ĻĖ░ļ░śņØä ļ¦łļĀ©ĒĢśĻ│Āņ×É ĒĢśņśĆļŗż.
ĻĄÉņĀĢņ╣śļŻīļź╝ ņ£äĒĢ┤ ņä£ņÜĖļīĆĒĢÖĻĄÉ ņ╣śĻ│╝ļ│æņøÉ ņåīņĢäņ╣śĻ│╝ņŚÉ ļé┤ņøÉĒĢ£ 6 - 13ņäĖ ņé¼ņØ┤ ĒÖśņĢä ņżæ ņĖĪļ░®ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦äņØä ņ┤¼ņśüĒĢśĻ│Ā 1ĻĖē ļČĆņĀĢĻĄÉĒĢ®ņ£╝ļĪ£ ņ¦äļŗ© ļ░øņØĆ ĒÖśņĢäļź╝ ļīĆņāüņ£╝ļĪ£ ņŚ░ĻĄ¼ļź╝ ņ¦äĒ¢ēĒĢśņśĆļŗż.
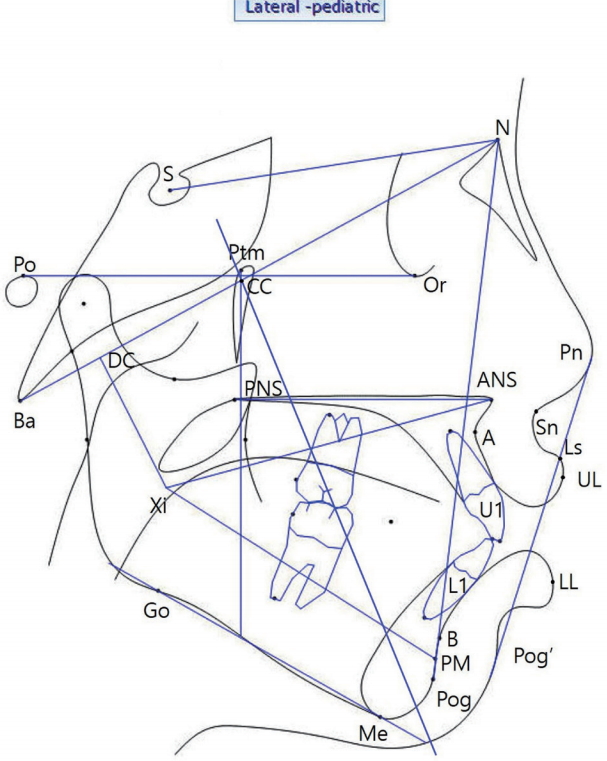
ļ│ĖņøÉ ņśüņāüņ╣śņØśĒĢÖĻ│╝ņŚÉņä£ ĒÖĢļīĆņ£©ņØ┤ ņĢĮ 110%ņØĖ ņןļ╣ä(Toshiba, DRX-61A)ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ņé¼ņ¦äņØä ņ┤¼ņśüĒĢ£ Ēøä V-ceph 5.5(Osstem, Seoul, Korea)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņĖĪņØä ĒĢ£ ĒÖśņĢä 100ļ¬ģņØś ļŹ░ņØ┤Ēä░ļź╝ ņłśņ¦æĒĢśņśĆļŗż. ļČäņäØņŚÉ ņé¼ņÜ®ļÉ£ Ļ│äņĖĪņĀÉĻ│╝ ļČäņäØĒĢŁļ¬® Fig. 1Ļ│╝ Table 1ņŚÉ ļéśĒāĆļéś ņ׳ņ£╝ļ®░, Ļ░üļÅä ņĖĪņĀĢņØĆ 0.01┬░Ļ╣īņ¦Ć, ĻĖĖņØ┤ ņĖĪņĀĢņØĆ 0.01 mmĻ╣īņ¦Ć ņŗ£Ē¢ēĒĢśņśĆļŗż.
ĻĖĖņØ┤, Ļ░üļÅä ļō▒ņŚÉ ļīĆĒĢ£ Ļ│äņĖĪĻ░ÆņØ┤ ņ׳ļŖö phantom ņןļ╣äņØś ļæÉļČĆ Ļ│äņĖĪļ░®ņé¼ņäĀ ņśüņāüņØä ņ┤¼ņśüĒĢ£ Ēøä, ļ│Ė ļ│æņøÉņŚÉņä£ ņé¼ņÜ®ĒĢśĻ│Ā ņ׳ļŖö ņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ phantom ņןļ╣ä ņ┤¼ņśü ņśüņāüņØä Ļ│äņĖĪĒĢ£ Ļ░ÆĻ│╝ phantom ņןļ╣äņØś Ļ│äņĖĪĻ░ÆņØä ļ╣äĻĄÉĒĢśļ®┤ ĻĄÉņĀĢĻ░Æ(correction value)ņØä Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ Ēæ£ņżĆĻ│╝ĒĢÖĻĖ░ņłĀņøÉ ņØśļŻīņ£ĄĒĢ®ņĖĪņĀĢĒæ£ņżĆņä╝Ēä░ņŚÉņä£ ļ░®ņé¼ņäĀ ņ┤¼ņśüņØ┤ Ļ░ĆļŖźĒĢ£ phantom ņןļ╣äļź╝ ņĀ£ņ×æĒĢśņśĆļŗż(Fig. 2A). ņØ┤ phantom ņןļ╣äļŖö Ļ░ĆļĪ£ 5Ļ░£, ņäĖļĪ£ 5Ļ░£ņØś Ļ░ĢĻĄ¼Ļ░Ć ĒżĒĢ©ļÉ£ ņĢäĒü¼ļ”┤ļ”Ł ļĀłņ¦äņ£╝ļĪ£ ņĀ£ņ×æĒĢśņśĆļŗż. ņ£äņÖĆ ļÅÖņØ╝ĒĢ£ ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņśüņāü ņ┤¼ņśü ņןļ╣äļĪ£ phantom ņןļ╣äņØś ļ░®ņé¼ņäĀ ņé¼ņ¦ä ņ┤¼ņśüņØä ĒĢśņśĆņ£╝ļ®░, ņØ┤ ļĢī Ļ┤ĆĻĄ¼ņŚÉņä£ phantom ņןļ╣äņØś Ļ▒░ļ”¼ļŖö 1500 mm, Ļ┤ĆĻĄ¼ņŚÉņä£ detectorĻ╣īņ¦ĆņØś Ļ▒░ļ”¼ļŖö 1660 mmņØ┤ņśĆļŗż(Fig. 2B). ņ¢╗ņ¢┤ņ¦ä ņśüņāüņØä V-ceph 5.5ņØä ņØ┤ņÜ®ĒĢ┤ Ļ░ĢĻĄ¼ ņé¼ņØ┤ņØś Ļ░üļÅäņÖĆ ĻĖĖņØ┤ļź╝ Ļ│äņĖĪĒĢśņśĆļŗż(Fig. 3). ņØ┤ Ļ░ÆņØä Ēæ£ņżĆĻ│╝ĒĢÖĻĖ░ņłĀņŚ░ĻĄ¼ņøÉņŚÉņä£ ņĀ£Ļ│ĄĒĢ┤ņżĆ phantomņŚÉņä£ Ļ░ĢĻĄ¼Ļ░äņØś ĻĖĖņØ┤ņÖĆ ņóīĒæ£ļź╝ ĒåĄĒĢ┤ Ļ│äņé░ļÉśļŖö Ļ│äņĖĪņĀÉ Ļ░äņØś Ļ░üļÅäņÖĆ ļ╣äĻĄÉĒĢśņśĆņ£╝ļ®░, ĒÖĢļīĆņ£©(1660/1500 ŌēÆ 1.11)ņØä Ļ│ĀļĀżĒĢśņŚ¼ ĻĄÉņĀĢĻ░ÆņØä Ļ│äņé░ĒĢśņśĆļŗż.
ļČłĒÖĢļÅäļŖö AĒśĢ ļČłĒÖĢļÅäņÖĆ BĒśĢ ļČłĒÖĢļÅäļĪ£ ļČäļźśļÉ£ļŗż. AĒśĢ Ēæ£ņżĆļČłĒÖĢļÅäļŖö ļ░śļ│Ą ņĖĪņĀĢĻ░ÆņØś ļ╣łļÅä ļČäĒżņŚÉ ĻĘ╝Ļ▒░ĒĢ£ ĒÖĢļźĀļ░ĆļÅäĒĢ©ņłśņŚÉņä£ ĻĄ¼ĒĢśļŖö ļ░śļ®┤, BĒśĢ Ēæ£ņżĆļČłĒÖĢļÅäļŖö ĻĖ░ņĪ┤ņØś ņĀĢļ│┤ ļśÉļŖö ļ¼ĖĒŚīņØä ĒåĄĒĢ┤ ņĖĪņĀĢĻ░ÆņØ┤ Ļ░Ćņ¦ł ņłś ņ׳ļŖö ĒÖĢļźĀļ░ĆļÅäĒĢ©ņłśļź╝ Ļ░ĆņĀĢĒĢśņŚ¼ ĻĄ¼ĒĢ£ļŗż[1].
ļČłĒÖĢļÅäļź╝ ņĖĪņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ Ļ░Ćņן ņżæņÜöĒĢ£ Ļ▓āņØĆ ņĖĪņĀĢļ¤ēņØä ĻĄ¼ņ▓┤ņĀüņ£╝ļĪ£ ņäżņĀĢĒĢśļŖö Ļ▓āņØ┤ļŗż. ņĖĪņĀĢ Ļ▓░Ļ│╝ņØś ļČłĒÖĢņŗżņä▒ņØä ņ£Āļ░£ĒĢĀ ņłś ņ׳ļŖö ņÜöņØĖņØä ņĀĢĒÖĢĒ׳ ņäżņĀĢĒĢśļŖö Ļ▓āņØĆ ņĖĪņĀĢĻ▓░Ļ│╝ņØś ļČłĒÖĢļÅäļź╝ ņĀĢĒÖĢĒ׳ ņĖĪņĀĢĒĢśļŖöļŹ░ ņ׳ņ¢┤ ļ░śļō£ņŗ£ ĒĢäņÜöĒĢśļ®░, ņĖĪņĀĢĻ▓░Ļ│╝ņØś ļ▓öņ£äļź╝ ļ│┤ļŗż ņĀĢĒÖĢĒ׳ ņśłņĖĪĒĢśļŖö Ļ▓āņØä Ļ░ĆļŖźĒĢśĻ▓ī ĒĢ£ļŗż.
ĻĄÉņĀĢĻ│äņĖĪņ╣ś ņĖĪņĀĢļ¤ēņØĆ ņĖĪļ░®ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦äņØä ņ┤¼ņśüĒĢśĻ│Ā ļé£ ņØ┤ĒøäņŚÉ ņĖĪņĀĢĒĢśļ»ĆļĪ£ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ēæ£ĒśäļÉĀ ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£ LeļŖö ņĖĪņĀĢļÉ£ ĻĄÉņĀĢĻ│äņĖĪĻ░Æ, LcļŖö ĻĄÉņĀĢĻ│äņĖĪĻ░Æ, cļŖö ņĖĪņĀĢņŗ£ņŖżĒģ£ņØś Ļ│äĒåĄņĀü ĒÜ©Ļ│╝ņØś ļ│┤ņĀĢņŚÉ ļīĆĒĢ£ ļČłĒÖĢļÅäņØ┤ļŗż.
AĒśĢ ļČłĒÖĢļÅäļŖö ņŚ░ņåŹņĀüņØĖ ņĖĪņĀĢņØä ĒåĄĒĢ┤ ņ¢╗ņØĆ Ļ┤ĆņĖĪĻ░ÆņØä ĒåĄĻ│äņĀüņ£╝ļĪ£ ļČäņäØĒĢśņŚ¼ ņé░ņČ£ĒĢĀ ņłś ņ׳ļŗż[1].
ŌæĀ ņĖĪņĀĢĻ▓░Ļ│╝ņØś ļČłĒÖĢļÅä(UA1)
ņ┤Ø 100ļ¬ģņØś ņåīņĢä ĒÖśņ×ÉņØś ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØä V-ceph ņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņĖĪņĀĢĒĢśņśĆņ£╝ļ®░ Ēæ£ņżĆĒÄĖņ░©ļź╝ AĒśĢ Ēæ£ņżĆļČłĒÖĢļÅäļĪ£ ņé¼ņÜ®ĒĢśņśĆļŗż.
ŌæĪ ļ░śļ│ĄņĖĪņĀĢņØś ļČłĒÖĢļÅä(UA2)
ļÅÖņØ╝ ĒÖśņ×ÉņŚÉņä£ Ļ│äņĖĪņĀÉņØä 10ļ▓ł ļ░śļ│Ą ņĖĪņĀĢĒĢśņŚ¼ Ēæ£ņżĆņśżņ░©ļź╝ AĒśĢ ļČłĒÖĢļÅäļĪ£ ņé¼ņÜ®ĒĢśņśĆļŗż.
BĒśĢ Ēæ£ņżĆļČłĒÖĢļÅäļŖö ņĖĪņĀĢļ¤ēņØ┤ ņĪ┤ņ×¼ĒĢĀ Ļ░ĆļŖźņä▒ņØ┤ ļåÆņØĆ ĒÖĢļźĀ ļČäĒżļź╝ ņČöņĀĢĒĢ£ Ēøä, ņØ┤ ĒÖĢļźĀ ļČäĒżņØś Ēæ£ņżĆĒÄĖņ░©ļź╝ Ļ│äņé░ĒĢśņŚ¼ ņé░ņČ£ĒĢĀ ņłś ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī ņØ╝ļ░śņĀüņ£╝ļĪ£ ņĀĢļ░ĆņĖĪņĀĢņŚÉņä£ļŖö ņĖĪņĀĢļ¤ēņØ┤ ņ¢┤ļ¢ĀĒĢ£ ļČäĒżļź╝ Ļ░Ćņ¦ĆļŖöņ¦ĆņŚÉ ļīĆĒĢ£ ņĀĢļ│┤Ļ░Ć ņČ®ļČäĒĢśņ¦Ć ņĢŖĻ│Ā, ņ×ģļĀźļ¤ēņØś ĒĢ£Ļ│äĻ░Æ(a)ļ¦ī ņČöņĀĢņØ┤ Ļ░ĆļŖźĒĢ£ Ļ▓ĮņÜ░Ļ░Ć ņ׳ļŗż. ņØ┤ļ¤░ Ļ▓ĮņÜ░ ĻĘĖ ĻĄ¼Ļ░ä ļé┤ņŚÉņä£ļŖö ņ×ģļĀźļ¤ēņØ┤ ņĪ┤ņ×¼ĒĢĀ ĒÖĢļźĀņØ┤ Ļ░ÖļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņŚ¼ ĻĘĀļō▒ ļČäĒż(uniform distribution) ņ”ē, ņ¦üņé¼Ļ░üĒśĢ(rectangular) ļČäĒżļź╝ Ļ░ĆņĀĢĒĢ£ļŗż[1]. ņ×ģļĀźļ¤ēņØ┤ ĒĢ£Ļ│äĻ░ÆņØ┤ aņØĖ ĻĘĀļō▒ ļČäĒżļź╝ ļö░ļź╝ ļĢī ņØ┤ ĒÖĢļźĀ ļČäĒżņØś Ēæ£ņżĆĒÄĖņ░©ļź╝ ņŗØņØä ĒåĄĒĢ┤ ņ£ĀļÅäĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░Öņ£╝ļ®░, ņØ┤ļŖö BĒśĢ Ēæ£ņżĆļČłĒÖĢļÅäĻ░Ć ļÉ£ļŗż[1].
ŌæĀ ņĄ£ņåī ļČäĒĢ┤ļŖźņ£╝ļĪ£ ļ░£ņāØĒĢśļŖö ļČłĒÖĢļÅä(UB1)
ņĖĪņĀĢĻ▓░Ļ│╝ļŖö ņåīņłśņĀÉ ļæśņ¦Ė ņ×Éļ”¼Ļ╣īņ¦Ć Ēæ£ņŗ£Ļ░Ć ļÉśļŖöļŹ░, ņØ┤ ļĢī ņĖĪņĀĢ Ļ▓░Ļ│╝ļĪ£ ļéśĒāĆļéśļŖö ņåīņłśņĀÉ ņĢäļל Ļ░ÆņØĆ ļŹö ļ¦ÄņØĆ ņ£ĀĒÜ©ņł½ņ×ÉļĪ£ ļéśĒāĆļé╝ ņłś ņ׳ļŖö ļ¼┤ĒĢ£ĒĢ£ Ļ░ÆņØś ļ░śņś¼ļ”╝ Ļ░ÆņØ┤ļŗż. ļö░ļØ╝ņä£ ņĄ£ņåī ļČäĒĢ┤ļŖź(ņĄ£ņåī ļłłĻĖł)ņ£╝ļĪ£ ņØĖĒĢ┤ ļ░£ņāØĒĢśļŖö ļČłĒÖĢņŗżņä▒ņØä ļČłĒÖĢļÅä Ļ│äņé░ ņŗ£ ĒżĒĢ©ĒĢśņŚ¼ņĢ╝ ĒĢ£ļŗż[1]. ĻĖĖņØ┤ņØś Ļ▓ĮņÜ░ ņĄ£ņåī ļČäĒĢ┤ļŖźņØ┤ 0.01 mmņØ┤Ļ│Ā, Ļ░üļÅäņØś Ļ▓ĮņÜ░ņŚÉļŖö 0.01┬░ņØ┤ļ»ĆļĪ£ ĻĖĖņØ┤ņØś ļČäĒĢ┤ļŖźņØĆ Ļ░üĻ░ü - 0.005 mmņŚÉņä£ + 0.005 mmņØś ļČłĒÖĢļÅäļź╝ ņĢ╝ĻĖ░ĒĢśĻ│Ā, Ļ░üļÅäņØś ļČäĒĢ┤ļŖźņØĆ - 0.005┬░ ņŚÉņä£ + 0.005┬░ņØś ļČłĒÖĢļÅäļź╝ ņĢ╝ĻĖ░ĒĢ£ļŗż. ņ”ē ĻĖĖņØ┤ņÖĆ Ļ░üļÅäļŖö Ļ░üĻ░ü 0.005 mm, 0.005┬░ņØś ļČłĒÖĢņŗżņä▒ņØä Ļ░Ćņ¦äļŗż. ĒÖĢļźĀļČäĒżļź╝ ņ¦üņé¼Ļ░üĒśĢ ļČäĒżļĪ£ Ļ░ĆņĀĢĒĢśņŚ¼ BĒśĢ ļČłĒÖĢļÅäļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.
ņØ┤ļź╝ ņåīņłśņĀÉ ļæśņ¦Ė ņ×Éļ”¼Ļ╣īņ¦Ć Ēæ£ĒśäĒĢśļ®┤ UB1ņØĆ ĻĖĖņØ┤ņÖĆ Ļ░üļÅä ļ¬©ļæÉ 0.00ņ£╝ļĪ£ ļéśĒāĆļé╝ ņłś ņ׳ļŗż.
ŌæĪ ļæÉļČĆĒÜīņĀä(angulation)ņ£╝ļĪ£ ņØĖĒĢ┤ ļ░£ņāØĒĢśļŖö ļČłĒÖĢļÅä(UB2)
ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ņé¼ņ¦ä ņ┤¼ņśü ņŗ£ņŚÉļŖö ļæÉļČĆņØś ĒÜīņĀäņ£╝ļĪ£ ņØĖĒĢ£ ņāüņØś ņÖ£Ļ│ĪņØ┤ ļ░£ņāØ ĒĢśņŚ¼ 3ņ░©ņøÉņØś ņ¢╝ĻĄ┤ ĒÅēļ®┤ņØ┤ 2ņ░©ņøÉņ£╝ļĪ£ Ēł¼ņśüļÉśļŖö Ļ│╝ņĀĢņŚÉņä£ ļČłĒÖĢļÅäļź╝ ņ£Āļ░£ĒĢĀ ņłś ņ׳ļŗż. ļö░ļØ╝ņä£ ņØ┤ļĪ£ ņØĖĒĢ£ ļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ┤ phantom ņןļ╣äļź╝ ņ£äņŚÉņä£ ļé┤ļĀżļŗż ļ┤żņØä ļĢī phantom ņןļ╣äņØś ĻĄ¼ņä▒ņÜöņåīĻ░Ć ņØ┤ļŻ©ļŖö Ļ░üļÅäĻ░Ć 90┬░Ļ░Ć ļÉśļÅäļĪØ ņĪ░ļ”ĮĒĢ£ ņāüĒā£ņŚÉņä£ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØä Ļ│äņé░ĒĢśņśĆļŗż(Fig. 4B, D). ņØ┤ļź╝ ņØ╝ņ¦üņäĀņ£╝ļĪ£ phantom ņןļ╣äļź╝ ņĀ£ņ×æĒĢ£ Ļ▓ĮņÜ░(Fig. 4A, C)ņÖĆ ļ╣äĻĄÉĒĢśņŚ¼, ĻĖĖņØ┤ļŖö 0.20 mm, Ļ░üļÅäļŖö 0.30┬░ņØś ņ░©ņØ┤ļź╝ ņ£Āļ░£ĒĢ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż.
ņØ┤ļĪĀņĀüņ£╝ļĪ£ angulationņØ┤ ļ░£ņāØĒĢĀ ņłś ņ׳ļŖö ĒÖĢļźĀņØĆ Ļ░üļÅäņØś ņĀĢļÅäņÖĆļŖö ļ¼┤Ļ┤ĆĒĢśĻ▓ī ņØ╝ņĀĢĒĢĀ Ļ▓āņØä Ļ░ĆņĀĢĒĢśņŚ¼ ĒÖĢļźĀļČäĒżļĪ£ ņ¦üņé¼Ļ░üĒśĢ ļČäĒżļź╝ Ļ░ĆņĀĢĒĢśņśĆĻ│Ā, ņØ┤ļź╝ ĒåĄĒĢ┤ ņĖĪņĀĢļÉśļŖö ĻĖĖņØ┤ņÖĆ Ļ░üļÅäņŚÉ ļīĆĒĢ£ BĒśĢ ļČłĒÖĢļÅäļŖö Ļ░üĻ░ü ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ļ│äņé░ĒĢśņśĆļŗż.
AĒśĢ ļČłĒÖĢļÅäņÖĆ BĒśĢ ļČłĒÖĢļÅäļŖö ĒĢ®ņä▒ņØ┤ Ļ░ĆļŖźĒĢśļ®░, ĻĘĖ Ļ▓░Ļ│╝ļĪ£ ļéśĒāĆļéśļŖö Ļ▓āņØ┤ ĒĢ®ņä▒Ēæ£ņżĆļČłĒÖĢļÅä(Uc)ņØ┤ļŗż. ņØ┤ļŖö ņĖĪņĀĢļīĆņāüņØś ņČöņĀĢĒæ£ņżĆĒÄĖņ░©ļź╝ ļéśĒāĆļé┤Ļ│Ā ļ¬©ļōĀ ņ×ģļĀźļ¤ēņØ┤ ļÅģļ”ĮņĀüņØĖ Ļ▓ĮņÜ░ Ļ│äņé░ļÉ£ AĒśĢ ļČłĒÖĢļÅäņÖĆ BĒśĢ ļČłĒÖĢļÅäļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņ¢╗ņØĆ Ļ░ÆņØś ņĀ£Ļ│▒ņØś ĒĢ®ņØś ņĀ£Ļ│▒ĻĘ╝ņØä ņĘ©ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż[1]. ĒÖĢņןļČłĒÖĢļÅä(UE)ļŖö ņĖĪņĀĢĻ░ÆņŚÉ ļīĆĒĢ┤ ĒĢ®ļ”¼ņĀü ņČöņĀĢĻ░ÆņØä ņØ┤ļŻ©ļŖö ļČäĒżņŚÉ ļīĆĒĢ┤ņä£ ņĖĪņĀĢĻ░ÆņØś ļīĆļČĆļČäņØ┤ ĒżĒĢ©ļÉĀ Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆļÉśļŖö ĻĄ¼Ļ░äņØä ņĀĢņØśĒĢ£ ņ¢æņØ┤ļŗż. ņØ┤ļŖö ĒĢ®ņä▒Ēæ£ņżĆļČłĒÖĢļÅäņŚÉ ĒÖĢņןņØĖņ×Éļź╝ Ļ│▒ĒĢśņŚ¼ ĻĄ¼ĒĢśņŚ¼ ņ¦äļŗż[1]. ļö░ļØ╝ņä£ ĒÖĢņןņØĖņ×É(k = 2, ņŗĀļó░ņłśņżĆ 95%)ļź╝ Ļ│▒ĒĢśņŚ¼ ĒÖĢņןļČłĒÖĢļÅäļź╝ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉ ĒżĒĢ©ļÉ£ ĒÖśņĢäņØś ļéśņØ┤ ļČäĒżļŖö 10ņäĖĻ░Ć 24ļ¬ģņ£╝ļĪ£ Ļ░Ćņן ļ¦ÄņĢśĻ│Ā, 11ņäĖ, 8ņäĖ, 9ņäĖ ņł£ņ£╝ļĪ£ ļ¦ÄņØĆ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé¼ļŗż(Table 2).
V-cephņØä ņØ┤ņÜ®ĒĢ┤ ņĖĪņĀĢĒĢ£ phantom ņןļ╣äņØś ļ░®ņé¼ņäĀ ņśüņāüņŚÉņä£ Ļ░ĢĻĄ¼ Ļ░äņØś ĻĖĖņØ┤ ĒÅēĻĘĀņØĆ 27.68 mmņØ┤ņśĆļŗż. Phantom ņןļ╣äņØś ņŗżņĀ£ ĻĖĖņØ┤ņÖĆ ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦äņØś ĒÖĢļīĆņ£©ņØä Ļ░ÉņĢłĒĢ£ Ļ░ĢĻĄ¼ Ļ░äņØś ĻĖĖņØ┤ļŖö ĒÅēĻĘĀ 27.72 mmņØ┤ņśĆļŗż. ņ”ē, V-cephņØä ĒåĄĒĢ┤ ņĖĪņĀĢļÉśļŖö ĻĖĖņØ┤Ļ░ÆņØĆ ņŗżņĀ£Ļ░Æļ│┤ļŗż 0.04 mm ņ×æĻ▓ī ņĖĪņĀĢļÉ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ĻĄÉņĀĢĻ░ÆņØĆ 0.04 mmļĪ£ Ļ│äņé░ļÉśņŚłļŗż.
phantom ņןļ╣äņØś ļ░®ņé¼ņäĀ ņśüņāüņØä V-cephņØä ĒåĄĒĢ┤ Ļ░üļÅäļź╝ ņĖĪņĀĢĒĢśņŚ¼ ĒÅēĻĘĀ 44.82┬░Ļ░ÆņØä ņ¢╗ņŚłļŗż. Phantom ņןļ╣ä Ļ░üļÅäļŖö ĒÅēĻĘĀ 44.93┬░ņ£╝ļĪ£, V-cephņØä ĒåĄĒĢ┤ ņĖĪņĀĢļÉśļŖö Ļ░üļÅäĻ░ÆņØĆ ņŗżņĀ£Ļ░Æļ│┤ļŗż 0.11┬░ ņ×æĻ▓ī ņĖĪņĀĢļÉ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ĻĄÉņĀĢĻ░ÆņØĆ 0.11┬░ņ×äņØä ņĢī ņłś ņ׳ņŚłļŗż.
ņĢ×ņä£ ņĀ£ņĢłļÉ£ ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢ£ ļČłĒÖĢļÅäļŖö Table 3ņŚÉ ļéśĒāĆļéś ņ׳ļŗż.
ņØ┤ņāüņØś Ļ▓░Ļ│╝ļź╝ ņóģĒĢ®ĒĢśņŚ¼ ļ│╝ ļĢī 1ĻĖē ļČĆņĀĢĻĄÉĒĢ®ņØä Ļ░Ćņ¦ä ļ¦ī 6 - 13ņäĖ ņé¼ņØ┤ ņåīņĢäņØś ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś standard referenceļŖö 95% ņŗĀļó░ĻĄ¼Ļ░äņŚÉņä£ ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ēæ£ļĪ£ ņĀĢļ”¼Ļ░Ć ļÉ©ņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż(Table 4). ļŗżļź┤Ļ▓ī Ēæ£ĒśäĒĢśļ®┤, ņä£ņÜĖļīĆĒĢÖĻĄÉ ņ╣śĻ│╝ļ│æņøÉņŚÉņä£ ņé¼ņÜ®ĒĢśļŖö ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņśüņāü ņ┤¼ņśüņןļ╣äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņ┤¼ņśüĒĢ£ ļ░®ņé¼ņäĀ ņśüņāüņØä V-ceph ĒöäļĪ£ĻĘĖļשņ£╝ļĪ£ ļČäņäØĒĢ£ ļ¦ī 6 - 13ņäĖ ņåīņĢäņŚÉņä£ņØś ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØĆ 95%ņØś ņŗĀļó░ļÅäļĪ£ Table 4ņŚÉņä£ Ēæ£ņŗ£ĒĢ£ ļ▓öņ£ä ļé┤ņŚÉ ļČäĒżĒĢ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż.
ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņśüņāüņØä ĒŖĖļĀłņØ┤ņŗ▒(tracing)ĒĢśĻ│Ā ļČäņäØĒĢ©ņŚÉ ņ׳ņ¢┤ņä£ ņĀĢĒÖĢņä▒Ļ│╝ ļåÆņØĆ ņ×¼Ēśäņä▒ņØĆ ĒĢäņłśņĀüņØĖ ņÜöņåīņØ┤ļŗż[14]. ņØ┤ņĀäņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļööņ¦ĆĒäĖ ņśüņāüņØä ņØ┤ņÜ®ĒĢ£ ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ļČäņäØ ĒöäļĪ£ĻĘĖļשņØś ņĀĢĒÖĢņä▒Ļ│╝ ņŗĀļó░ļÅäļź╝ ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢ┤ ņĀäĒåĄņĀüņØĖ hand tracingņØä ĒåĄĒĢ┤ ĻĄ¼ĒĢ£ Ļ│äņĖĪĻ░ÆĻ│╝ ĒöäļĪ£ĻĘĖļשņØä ņØ┤ņÜ®ĒĢ£ ņ¢╗ņØĆ Ļ│äņĖĪĻ░ÆņØä ļ╣äĻĄÉĒĢśļŖö ļ░®ļ▓ĢņØä ļ¦ÄņØ┤ ņé¼ņÜ®ĒĢśņśĆļŗż[10,11,15-17]. ĻĘĖ Ļ▓░Ļ│╝ ņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ņØ┤ņÜ®ĒĢ£ ļ░®ņŗØņØ┤ ņĀäĒåĄņĀüņØĖ ļ░®ļ▓ĢĻ│╝ ņ£Āņé¼ĒĢ£ ņĀĢļÅäņØś ņ×¼Ēśäņä▒Ļ│╝ ņĀĢĒÖĢļÅäļź╝ Ļ░Ćņ¦ĆļŖö Ļ▓āņØ┤ ļ│┤Ļ│Ā ļÉśĻ│Ā ņ׳ļŗż[10,17]. ļ░śļ®┤ ņ×¼Ēśäņä▒ņØ┤ļéś ņĀĢĒÖĢņä▒ņŚÉņä£ ņĀäĒåĄņĀüņØĖ ļ░®ļ▓ĢĻ│╝ ņ£ĀņØśĒĢ£ ņ░©ņØ┤Ļ░Ć ņ׳ņ¦Ćļ¦ī ņ×äņāüņĀüņ£╝ļĪ£ ņ£ĀņØśĒĢ£ ņ░©ņØ┤Ļ░Ć ņŚåļŗżĻ│Ā ĒĢ£ ņŚ░ĻĄ¼ļÅä ņĪ┤ņ×¼ĒĢ£ļŗż[15,16]. ĒĢśņ¦Ćļ¦ī ņØ┤ņĀäņØś ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉ£ ļ░®ņé¼ņäĀ ņ┤¼ņśüņןļ╣ä, ļČäņäØĒöäļĪ£ĻĘĖļשņØś Ļ▓ĮņÜ░ ņåīĻĖēņä▒ņØ┤ ĒÖĢļ│┤ļÉśņ¦Ć ņĢŖņĢśļŗż. ņåīĻĖēņä▒ņØ┤ ĒÖĢļ│┤ļÉśņ¦Ć ņĢŖņØĆ ņןļ╣ä, ļČäņäØĒöäļĪ£ĻĘĖļשņŚÉņä£ ņĖĪņĀĢļÉ£ Ļ▓░Ļ│╝ļŖö ņĀĢĒÖĢĒĢ£ Ļ│äņĖĪĻ░ÆņØä ļ░śņśüĒĢśņ¦Ć ļ¬╗ĒĢ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĻĖĖņØ┤ņÖĆ Ļ░üļÅäņŚÉ ļīĆĒĢ£ Ļ│äņĖĪĻ░ÆņØ┤ ņŗżņĀ£Ļ░Æļ│┤ļŗż 0.04 mm, 0.11┬░ ņ×æĻ▓ī ņĖĪņĀĢļÉ©ņØä ĒÖĢņØĖĒĢśņśĆĻ│Ā, ņØ┤ļź╝ ĻĄÉņĀĢĻ░ÆņØä ĒåĄĒĢ┤ ļ│┤ņĀĢĒĢśņśĆļŗż. ĒĢśņ¦Ćļ¦ī ņØ┤ņĀäņØś ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉ£ ļ░®ņé¼ņäĀ ņ┤¼ņśüņןļ╣ä, ļČäņäØ ņåīĒöäĒŖĖņø©ņ¢┤Ļ░Ć ļ│Ė ņŚ░ĻĄ¼ņÖĆ ļÅÖņØ╝ĒĢśņ¦ĆļŖö ņĢŖļŗż. ļ¦īņĢĮ ņĖĪņĀĢĻ░ÆņØ┤ ņŗżņĀ£Ļ░ÆņØä Ļ│╝ļÅäĒĢśĻ▓ī Ļ│╝ņĖĪņĀĢ(overestimation) ĒĢ£ļŗżļ®┤ ļČäņäØņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ĒåĄĒĢ┤ ĻĄ¼ĒĢ┤ņ¦ĆļŖö ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØĆ ņŗżņĀ£ Ļ░Æļ│┤ļŗż Ēü¼Ļ▓ī ļÉ£ļŗż. ļ░śļīĆļĪ£ ņŗżņĀ£Ļ░ÆņØä ņĀĆņĖĪņĀĢ(underestimation) ĒĢ£ļŗżļ®┤ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØĆ ņŗżņĀ£ Ļ░Æļ│┤ļŗż ņ×æņØĆ Ļ░ÆņØä Ļ░Ćņ¦äļŗż. ļö░ļØ╝ņä£ ņŗżņĀ£Ļ░ÆņØä ļ░śņśüĒĢśĻĖ░ ņ£äĒĢ┤ ĻĄÉņĀĢĻ░ÆņØä ļ░śņśüĒĢĀ ĒĢäņÜöĻ░Ć ņ׳ļŗż. ļö░ļØ╝ņä£ ņØ┤ņĀäņØś ņŚ░ĻĄ¼ņŚÉņä£ ĻĄ¼ĒĢ£ Ļ│äņĖĪĻ░ÆņØś Ļ▓ĮņÜ░ ņןļ╣ä ļ░Å ļČäņäØņåīĒöäĒŖĖņø©ņ¢┤ņØś ņåīĻĖēņä▒ņØä ĒÖĢļ│┤ĒĢśĻ│Ā ļé£ ĒøäņØś ĻĄÉņĀĢĻ░ÆņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņĖĪĻ░ÆņŚÉ ļ░śņśüĒĢĀ ĒĢäņÜöĻ░Ć ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņāØĻ░üļÉ£ļŗż.
ņØ┤ļ▓ł ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņåīĻĖēņä▒ņØ┤ ĒÖĢļ│┤ļÉ£ phantom ņןļ╣äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņåīĒöäĒŖĖņø©ņ¢┤ņØś ņĀĢĒÖĢņä▒ņØä ĒÅēĻ░ĆĒĢśņśĆļŗżļŖö ņĀÉņŚÉņä£ ĻĖ░ņĪ┤ ņŚ░ĻĄ¼ņÖĆ ņ░©ņØ┤ņĀÉņØä Ļ░Ćņ¦äļŗż. Ēæ£ņżĆĻ│╝ĒĢÖņŚ░ĻĄ¼ņøÉņŚÉņä£ Ēæ£ņżĆĒÖöļÉ£ Ļ│╝ņĀĢņØä Ļ▒░ņ│Éņä£ ņĀ£ņ×æļÉ£ phantom ņןļ╣ä ņ×Éņ▓┤ņØś ĻĖĖņØ┤, Ļ░üļÅä Ļ░ÆĻ│╝ ĒöäļĪ£ĻĘĖļשņØä ņØ┤ņÜ®ĒĢ┤ ņŗżņĀ£ ņĖĪņĀĢĒĢ£ Ļ▒░ļ”¼ ļ░Å Ļ░üļÅäļź╝ ļ╣äĻĄÉĒĢśņŚ¼ ĻĄÉņĀĢĻ░ÆņØä ĻĄ¼ĒĢśņśĆĻ│Ā, ņØ┤ļź╝ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś ļ▓öņ£äļź╝ ņČöņĀĢĒĢśļŖö ļŹ░ ĒÖ£ņÜ®ĒĢśņśĆļŗż. ĻĄÉņĀĢĻ░ÆņØĆ ĻĖĖņØ┤ 0.04 mm, Ļ░üļÅä 0.11┬░ļĪ£ ļéśĒāĆļé¼ļŗż. ņØ┤ļŖö ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ņé¼ņ¦ä Ļ│äņĖĪ ņŗ£ ┬▒ 0.81 mmņØś ņśżņ░©ļŖö ļ░øņĢäļōżņŚ¼ņ¦ł ņłś ņ׳ļŗżļŖö ĻĖ░ņĪ┤ ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉĒĢ┤ ļ│╝ ļĢī Ēśäņ×¼ ļ│ĖņøÉņŚÉņä£ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŖö ņןļ╣ä ļ░Å ļČäņäØ ņåīĒöäĒŖĖņø©ņ¢┤ņØś Ļ▓ĮņÜ░ ĻĄÉņĀĢņØ┤ ļ¦żņÜ░ ņל ņØ┤ļŻ©ņ¢┤ņĀĖ ņ׳ņ£╝ļ®░, ļåÆņØĆ ņŗĀļó░ļÅäļź╝ Ļ░Ćņ¦ĆĻ│Ā ņ׳ņØīņØä ņØśļ»ĖĒĢ£ļŗż[18]. ĒĢśņ¦Ćļ¦ī ļ│æņøÉļ¦łļŗż ņé¼ņÜ®ĒĢśļŖö ņśüņāüņןļ╣äņØś ņóģļźśĻ░Ć ļŗżļź┤Ļ│Ā Ļ░ü ņןļ╣äļ¦łļŗż ņśüņāü ņ┤¼ņśüļ░®ļ▓ĢĻ│╝ ņśüņāüĒÜŹļōØļ░®ļ▓ĢņØ┤ ņ░©ņØ┤Ļ░Ć ļéśļ®░, ļČäņäØĒöäļĪ£ĻĘĖļשņØś Ļ│äņé░ ņĢīĻ│Āļ”¼ņ”śņØ┤ ņāüņØ┤ĒĢśļ»ĆļĪ£ ļ│Ė ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ĻĄ¼ĒĢ£ ĻĄÉņĀĢĻ░ÆĻ│╝ ņ░©ņØ┤Ļ░Ć ļéĀ ņłś ņ׳ņ£╝ļ®░, ņØ┤ļŖö ļČäņäØņåīĒöäĒŖĖņø©ņ¢┤ņØś Ļ░£ļ░£ ļ░Å ņłśņĀĢņØä ĒåĄĒĢ┤ Ļ░£ņäĀļÉĀ ņłś ņ׳ņØä Ļ▓āņØ┤ļŗż. ļśÉĒĢ£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ĒĢ£ Ļ│ĄņØĖļÉ£ phantom ņןļ╣äļź╝ ņØ┤ņÜ®ĒĢ┤ ļČäņäØņåīĒöäĒŖĖņø©ņ¢┤ņØś ņåīĻĖēņä▒ņØä ĒÖĢļ│┤ĒĢśĻ│Ā ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ ĻĄÉņĀĢĻ░ÆņØä ļ░śņśüĒĢśļŖö ņ▓śļ”¼Ļ│╝ņĀĢņØ┤ ĒĢäņÜöĒĢśļ”¼ļØ╝ ņāØĻ░üļÉ£ļŗż.
ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦ä ļČäņäØņŚÉ ņ׳ņ¢┤ ļéśĒāĆļéĀ ņłś ņ׳ļŖö ņśżļźśļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ Ļ│äĒåĄ ņśżņ░©(systematic error)ņÖĆ ņÜ░ņŚ░ ņśżņ░©(random error)Ļ░Ć ņ׳ļŗż. Ļ│äĒåĄ ņśżņ░©ņŚÉļŖö ņśüņāüņØś ĒÖĢļīĆ, ļŗżļźĖ ĒÅēļ®┤ņāüņŚÉ ņ£äņ╣śĒĢ£ ļ¼╝ņ▓┤ļōżņØś ĒÖĢļīĆņ£© ņ░©ņØ┤ļĪ£ ņØĖĒĢ£ ņāüņØś ņÖ£Ļ│Ī ļō▒ņØ┤ ņ׳ļŗż. ņÜ░ņŚ░ ņśżņ░©ļŖö ņŻ╝ļĪ£ ļ░®ņé¼ņäĀĒĢÖņĀü Ļ│äņĖĪņĀÉņØä ņ░ŠņĢäļé┤ļŖö Ļ│╝ņĀĢņŚÉņä£ņØś ļČłĒÖĢņŗżņä▒ņŚÉņä£ ņŻ╝ļĪ£ ĻĖ░ņØĖĒĢ£ļŗż[19]. ņØ┤ļ¤¼ĒĢ£ ņśżļźśļōżņØĆ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØä ĻĄ¼ĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ ļ¦ÄņØĆ ļČłĒÖĢņŗżņä▒ņØä ņ£Āļ░£ĒĢśļŖö ļ│ĆņłśļĪ£ ņ×æņÜ®ĒĢ£ļŗż. ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ļČäņäØ ņŗ£ņŚÉļŖö ņĖĪņĀĢĻ░ÆņØä Ļ│äņé░ĒĢśļŖö Ļ│╝ņĀĢ ņżæņŚÉ ļéśĒāĆļéĀ ņłś ņ׳ļŖö ņØ┤ļ¤¼ĒĢ£ ņÜöņåīļź╝ Ļ│ĀļĀżĒĢ┤ņĢ╝ ĒĢśļ®░, ļČłĒÖĢņŗżņä▒ņØä ņ£Āļ░£ĒĢĀ ņłś ņ׳ļŖö ļ¬©ļōĀ ņÜöņØĖņØä Ļ│ĀļĀżĒĢśĻ▓ī ļÉśļ®┤ ļÅÖņØ╝ĒĢ£ ņĖĪņĀĢņØä ļ░śļ│ĄĒĢśļŖö Ļ▓ĮņÜ░ ņĖĪņĀĢĻ░ÆņØś ļ▓öņ£äļź╝ ņŗĀļó░ļÅä ņ׳Ļ▓ī ĒÅēĻ░ĆĒĢĀ ņłś ņ׳ļŗż.
ĻĖ░ņĪ┤ņØś ņŚ░ĻĄ¼ļŖö ļČäņäØņåīĒöäĒŖĖņø©ņ¢┤ļź╝ ĒåĄĒĢ┤ ĻĄ¼ĒĢ┤ņ¦ä Ļ│äņĖĪĻ░ÆņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĻĄÉņĀĢĻ│äņĖĪņ╣śņØś ņČöņĀĢĻ░ÆņØä Ļ│äņé░ĒĢśņśĆļŗż. ĒĢśņ¦Ćļ¦ī ņĖĪņĀĢĻ░ÆņØ┤ Ļ│äņé░ļÉśļŖö Ļ│╝ņĀĢņŚÉņä£ ņłśņŚåņØ┤ ļ¦ÄņØĆ ļČłĒÖĢņŗżņä▒ņØä ņ£Āļ░£ĒĢśļŖö ņÜöņåīĻ░Ć ņ׳ņ£╝ļ®░, ņØ┤ņÖĆ Ļ░ÖņØĆ ļČłĒÖĢņŗżņä▒ņØĆ ņĖĪņĀĢĻ░ÆņØś Ļ▓░Ļ│╝ļź╝ ņÖ£Ļ│Īņŗ£Ēé¼ ņłś ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĖĪņĀĢĻ░ÆņØś ļČłĒÖĢņŗżņä▒ņØä ņ£Āļ░£ĒĢĀ ņłś ņ׳ļŖö ņÜöņØĖņ£╝ļĪ£ ļ░śļ│ĄņĖĪņĀĢņØä ĒåĄĒĢ┤ ĻĄ¼ĒĢĀ ņłś ņ׳ļŖö AĒśĢ ļČłĒÖĢļÅä ņÜöņåīļŖö ļČäņäØĒöäļĪ£ĻĘĖļשņØś ļ░śļ│ĄņĖĪņĀĢ ļ░Å Ļ░£ņØĖĻ░ä ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś ņ░©ņØ┤ļź╝ Ļ│ĀļĀżĒĢśņśĆĻ│Ā, ņäĀĒŚśņĀü ĒÖĢļźĀļČäĒżļź╝ ĒåĄĒĢ┤ Ļ│äņé░ Ļ░ĆļŖźĒĢ£ BĒśĢ ļČłĒÖĢļÅä ņÜöņåīļŖö ņĄ£ņåī ļČäĒĢ┤ļŖź, 3ņ░©ņøÉ Ļ│ĄĻ░äņØ┤ 2ņ░©ņøÉņ£╝ļĪ£ Ēł¼ņśüļÉśļŖö Ļ│╝ņĀĢņŚÉņä£ ņāØĻĖ░ļŖö angulationņ£╝ļĪ£ ņØĖĒĢ£ ļČłĒÖĢļÅä, phantom ņןļ╣ä ņ×Éņ▓┤ņØś Ēæ£ņżĆļČłĒÖĢļÅäļź╝ Ļ│ĀļĀżĒĢśņśĆļŗż. Ļ░ü ļČłĒÖĢļÅä ņÜöņåīļź╝ ĒåĄĒĢ┤ Ļ│äņé░ļÉśļŖö ĒĢ®ņä▒ ļČłĒÖĢļÅäņŚÉ Ļ░£ņØĖĻ░ä ĻĄÉņĀĢĻ│äņĖĪĻ░Æ ĒÄĖņ░©Ļ░Ć Ļ░Ćņן Ēü░ ņśüĒ¢źņØä ļ»Ėņ╣śļŖö ņÜöņåīļĪ£ ņ×æņÜ®ĒĢ£ļŗżļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż. ņØ┤ļŖö ņåīņĢäņŚÉņä£ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØä Ļ│äņé░ĒĢśļŖö Ļ▓ĮņÜ░ Ļ│äņĖĪĻ░ÆņØ┤ ļČäĒżļÉśļŖö ļ▓öņ£äļź╝ Ļ▓░ņĀĢĒĢśļŖöļŹ░ ņ׳ņ¢┤ņä£ Ļ░£ņØĖĻ░ä ņ░©ņØ┤Ļ░Ć Ļ░Ćņן Ēü░ ņśüĒ¢źņØä ļ»Ėņ╣£ļŗżļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż. ņØ┤ņÖĖņŚÉ ļŗżļźĖ ļČłĒÖĢļÅä ņÜöņåīļŖö Ļ│äņĖĪĻ░ÆņØś ļČäĒż ļ▓öņ£äņŚÉ Ēü░ ņśüĒ¢źņØä ļü╝ņ╣śņ¦Ć ņĢŖļŖöļŗżļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż. ņØ┤ļŖö phantom ņןļ╣äņØś ļČłĒÖĢļÅäĻ░Ć ļ¦żņÜ░ ņ×æņØä ļ┐Éļ¦ī ņĢäļŗłļØ╝ ļČäņäØĒöäļĪ£ĻĘĖļשņŚÉņä£ Ļ│äņĖĪĻ░ÆņØä Ļ│äņé░ĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ Ļ│äņĖĪņĀÉņØä ņäĀņĀĢĒĢśļŖö ņ£äņ╣śņØś ļ│ĆĒÖöņŚÉ ļö░ļźĖ Ļ│äņĖĪĻ░ÆņØś ĒÄĖņ░© ļō▒ņØ┤ Ļ│äņĖĪĻ░ÆņØś ļČäĒżņ¢æņāüņŚÉ Ēü░ ņśüĒ¢źņØä ņŻ╝ņ¦Ć ņĢŖņØīņØä ņØśļ»ĖĒĢ£ļŗż. ļśÉĒĢ£ ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀ ņ┤¼ņśüĻ│╝ņĀĢ ņżæņŚÉ Ear rodņŚÉ ņ¢╝ĻĄ┤ņØä Ļ│ĀņĀĢ ņŗ£Ēé© ņāüĒā£ņŚÉņä£ ņ┤¼ņśüņØ┤ ņØ┤ļŻ©ņ¢┤ņĀĖņä£ ņØ┤ļĪ£ ņØĖĒĢ£ ļČłĒÖĢļÅä Ļ░ÆņØ┤ Ēü¼ņ¦Ć ņĢŖĻĖ░ ļĢīļ¼ĖņØ╝ Ļ▓āņ£╝ļĪ£ ņāØĻ░üļÉ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļæÉļČĆņØś ņ£äņ╣śļź╝ 90┬░ ĒÜīņĀäĒĢśņśĆņØä ļĢīļĪ£ Ļ░ĆņĀĢĒĢśņŚ¼ ņØ┤ļĪ£ ņØĖĒĢ£ ļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśņśĆņ£╝ļéś, Achlqvist ļō▒[20]ņØĆ ņĖĪļ░®ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņśüņāü ņ┤¼ņśü ņŗ£ 5┬░ ņØ┤ņāüņØś ņלļ¬╗ļÉ£ ļ©Ėļ”¼ ņ£äņ╣śļŖö ņēĮĻ▓ī ņĢī ņłś ņ׳Ļ│Ā, ļ░öļĪ£ ņĪ░ņĀĢņØ┤ Ļ░ĆļŖźĒĢśļŗżĻ│Ā ĒĢśņśĆļŗż. ļö░ļØ╝ņä£ ļæÉļČĆĒÜīņĀäņ£╝ļĪ£ ņØĖĒĢ£ ļČłĒÖĢļÅäļŖö ņŗżņĀ£ļĪ£ļŖö ļŹö ņ×æĻ▓ī ļéśĒāĆļéĀ Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż.
ļ│Ė ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ņÖĆ Ēśäņ×¼ ļ│ĖĻ│╝ņŚÉņä£ ņé¼ņÜ®ĒĢśĻ│Ā ņ׳ļŖö ņ░ĖĻ│Ā Ēæ£ņżĆņ╣śņÖĆ ļ╣äĻĄÉ ņŗ£ L1 to APo (degree), U1 to APo (degree), L1 to Mand.pl, interincisal angleĻ│╝ Ļ░ÖņØ┤ ņ╣śņĢäņÖĆ Ļ┤ĆļĀ©ļÉ£ Ļ│äņĖĪ ĒĢŁļ¬®ņØś ļ▓öņ£äĻ░Ć Ēü¼Ļ▓ī ļéśĒāĆļé¼ļŗż. ņØ┤ļŖö 1ĻĖē ļČĆņĀĢĻĄÉĒĢ®ņØś Ļ▓ĮņÜ░ Ļ│©Ļ▓®ņĀü ļČĆņĪ░ĒÖöļĪ£ ņØĖĒĢ£ ļČĆņĀĢĻĄÉĒĢ®ņØ┤ ņĢäļŗī ņ╣śņĢäņØś ņ£äņ╣śļĪ£ ņØĖĒĢ£ Ļ▓āņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ņØ┤ņÖĆ ņŚ░Ļ┤ĆļÉ£ Ļ░£ņØĖĻ░ä ĒÄĖņ░©Ļ░Ć Ēü¼Ļ▓ī ļéśĒāĆļé¼ĻĖ░ ļĢīļ¼ĖņØĖ Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż. ļśÉĒĢ£ 1ĻĖē ļČĆņĀĢĻĄÉĒĢ®ņØä ņ¦äļŗ©ĒĢśĻĖ░ ņ£äĒĢ┤ ĻĖ░ņĪ┤ ņ░ĖņĪ░Ēæ£ņżĆņØä ņØ┤ņÜ®ĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ Ļ│©Ļ▓®Ļ│╝ ņŚ░Ļ┤ĆļÉ£ Ļ│äņĖĪĻ░ÆņØś ļ▓öņ£äļŖö ĻĖ░ņĪ┤ ņ░ĖņĪ░Ēæ£ņżĆĻ│╝ Ēü░ ņ░©ņØ┤ļź╝ ļéśĒāĆļé┤ņ¦Ć ņĢŖņØĆ Ļ▓āņ£╝ļĪ£ ļ│┤ņØĖļŗż.
ņØ╝ļČĆ Ļ│äņĖĪĻ░ÆņØĆ ņŚ░ļĀ╣ņØ┤ ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ Ļ░ÉņåīĒĢśĻ▒░ļéś ņ”ØĻ░ĆĒĢĀ ņłś ņ׳ļŗż. Convexity, Facial depth, Mandibular plane angle, Mandibular arc, Corpus length, Upper molar positionņØĆ 9ņäĖļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ņä▒ņןĒĢ©ņŚÉ ļö░ļØ╝ 1ļģäņŚÉ Ļ░üĻ░ü - 0.2 mm, 0.3┬░, - 0.2┬░, 0.3┬░, 1.5 mm, 2 mmņö® ļ│ĆĒÖöĒĢśĻ▓ī ļÉ£ļŗż[21]. ĒĢśņ¦Ćļ¦ī ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņØ┤ņŚÉ ļīĆĒĢ£ Ļ│ĀļĀżĻ░Ć ļÉśņ¦Ć ņĢŖņĢśļŖöļŹ░ ņØ┤ļ¤¼ĒĢ£ ņĀÉņØ┤ ļ│Ė ņŚ░ĻĄ¼ņØś ĒĢ£Ļ│äņĀÉņØ┤ļŗż. ļö░ļØ╝ņä£ ņĀĢņāüĻĄÉĒĢ®ņØś ņ░ĖņĪ░Ēæ£ņżĆņØä ļ¦łļĀ©ĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņĀĢņāüĻĄÉĒĢ®ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņĢäņØ┤ļōżņØä ļīĆņāüņ£╝ļĪ£ ĒĢ£ ņĀäĒ¢źņĀü ņŚ░ĻĄ¼Ļ░Ć ĒĢäņÜöĒĢśļ®░, ņĪ░ņé¼ ļīĆņāü ņĢäļÅÖ ņłśļź╝ ļŖśļĀż ņČöĻ░ĆņĀü ņŚ░ĻĄ¼Ļ░Ć ņ¦äĒ¢ēļÉśņ¢┤ņĢ╝ ļÉĀ Ļ▓āņØ┤ļŗż.
ĻĄÉņĀĢ ņ╣śļŻī ņŗ£ ņ¦äļŗ©Ļ│╝ ņ╣śļŻī Ļ│äĒÜŹ ņłśļ”ĮņØä ņ£äĒĢ┤ ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦ä Ļ│äņĖĪ Ļ░ÆņØś Ļ│©Ļ▓®ņĀü ņĀĢņāü ļ▓öņŻ╝ļź╝ ņĢäļŖö Ļ▓āņØĆ ņżæņÜöĒĢśļŗż. ļ│Ė ņŚ░ĻĄ¼ļŖö ņĖĪņĀĢņןļ╣äņØś ņåīĻĖēņä▒ ļ░Å ļČłĒÖĢļÅäļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ĒĢ£ĻĄŁ ņåīņĢäņŚÉņä£ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś ļČäĒżļ▓öņ£äļź╝ ņĀĢĒÖĢĒĢśĻ▓ī ĻĄ¼ĒĢ£ ļŹ░ ņØśņØśĻ░Ć ņ׳ļŗż. 1ņ░© Ēæ£ņżĆņ£╝ļĪ£ ņé¼ņÜ®ņØ┤ Ļ░ĆļŖźĒĢ£ ļåÆņØĆ ņĀĢĒÖĢļÅäļź╝ ļéśĒāĆļé┤ļŖö Ļ│ĄņØĖļÉ£ phantom ņןļ╣äļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĻĄÉņĀĢĻ░ÆņØä ņČöņĀĢĒĢśņśĆĻ│Ā ņĖĪņĀĢ Ļ│äņĖĪĻ░ÆņØś ņĄ£ņäĀņØś ņČöņĀĢĻ░ÆņØś ļČäĒżļ▓öņ£äļź╝ ļČłĒÖĢņŗżņä▒ņØä ņ£Āļ░£ĒĢśļŖö ļ¬©ļōĀ ņÜöņåīļź╝ Ļ│ĀļĀżĒĢśņŚ¼ Ļ│äņé░ĒĢśņśĆļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņĀ£ņŗ£ļÉ£ Ļ░ÆņØĆ 1ĻĖē ņ╣śņä▒ļČĆņĀĢĻĄÉĒĢ®ņØä Ļ░Ćņ¦ä 6ņŚÉņä£ 13ņäĖ ņé¼ņØ┤ ĒĢ£ĻĄŁ ņåīņĢäņŚÉņä£ ņĖĪļ░®ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņé¼ņ¦ä Ļ│äņĖĪņØä ņŗ£Ē¢ēĒĢśļ®┤ 95%ņØś ņŗĀļó░ļÅäļĪ£ Ļ░ü Ļ│äņĖĪĻ░ÆņØ┤ ļČłĒÖĢļÅä ļČäĒżļ▓öņ£ä ļé┤ņŚÉ ņ£äņ╣śĒĢ©ņØä ņØśļ»ĖĒĢ£ļŗż. ļŗżņŗ£ ļ¦ÉĒĢśļ®┤, 100ļ¬ģņØś ņåīņĢäņŚÉņä£ ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØä ņĖĪņĀĢĒĢśļ®┤ ņĀüņ¢┤ļÅä 95ļ¬ģņØś ņåīņĢäņŚÉņä£ ņĖĪņĀĢļÉ£ Ļ│äņĖĪĻ░ÆņØĆ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ Ļ│äņé░ļÉ£ ļ▓öņ£ä ļé┤ņŚÉ ļČäĒżĒĢ©ņØä ņØśļ»ĖĒĢ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉśļŖö ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśļ®┤ ņČöĒøä ņĀĢņāüĻĄÉĒĢ® ĒÖśņĢäņØś ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś ļ▓öņ£äļź╝ ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ņ░ĖņĪ░Ēæ£ņżĆ ņäżņĀĢ ņŗ£ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņāØĻ░üļÉ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņä£ņÜĖļīĆĒĢÖĻĄÉ ņ╣śĻ│╝ļ│æņøÉņŚÉņä£ ņé¼ņÜ®ĒĢśĻ│Ā ņ׳ļŖö ļæÉļČĆĻ│äņĖĪļ░®ņé¼ņäĀņśüņāü ļČäņäØ ĒöäļĪ£ĻĘĖļשņØś ņåīĻĖēņä▒ņØä ĒÖĢļ│┤ĒĢśņŚ¼ ļČäņäØ ĒöäļĪ£ĻĘĖļשņØ┤ ļåÆņØĆ ņĀĢĒÖĢņä▒ ļ░Å ņŗĀļó░ļÅäļź╝ Ļ░Ćņ¦ÉņØä ņĢī ņłś ņ׳ņŚłĻ│Ā, ĻĄÉņĀĢĻ░ÆņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņĖĪĻ░ÆņØä ĻĄÉņĀĢĒĢśņśĆļŗż. ļśÉĒĢ£ ĻĄÉņĀĢņ╣śļŻīļź╝ ņŗ£ņ×æĒĢśļŖö ļ¦ī 6 - 13ņäĖ ņé¼ņØ┤ņØś ĒĢ£ĻĄŁņØĖ ņåīņĢäņŚÉņä£ņØś ĻĄÉņĀĢĻ│äņĖĪņ╣śņØś ļČłĒÖĢļÅäļź╝ Ļ│äņé░ĒĢśņŚ¼ 1ĻĖē ļČĆņĀĢĻĄÉĒĢ® ĒÖśņĢäņØś ĻĄÉņĀĢĻ│äņĖĪĻ░ÆņØś 95% ņŗĀļó░ļÅäļź╝ Ļ░Ćņ¦ĆļŖö ļČäĒżļ▓öņ£äļź╝ ņĀ£ņŗ£ĒĢśņśĆļŗż.
Fig┬Ā2.
(A) Phantom device used in this study. (B) Distance from phantom device to tube and detector.

Fig┬Ā3.
(A) Lateral cephalometric radiograph of phantom device. (B) Tracing and measure of phantom device using V-ceph program.

Fig┬Ā4.
(A) The original phantom device (view from above) and (B) its radiographic image. (C) The re-assembled phantom device so that the angle formed by each component is 90┬░ when viewed from above and (D) its radiographic image.

Table┬Ā1.
Cephalometric skeletal and dental measurements
Table┬Ā2.
Age distribution of the children included in this study
| Age | Number of person |
|---|---|
| 6 | 3 |
| 7 | 8 |
| 8 | 15 |
| 9 | 14 |
| 10 | 24 |
| 11 | 16 |
| 12 | 12 |
| 13 | 8 |
Table┬Ā3.
The mean, standard deviation, correction value, and uncertainty values obtained in this study
Table┬Ā4.
Standard reference of lateral cephalometric measurements of children with class I malocclusion (95% confidence interval)
References
1. Bureau international des Poids et Mesures : Evaluation of measurement data - Guide to the Expression of Uncertainty in Measurement JCGM 100:2008 (GUM 1995 with minor corrections). Available from URL: http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (Accessed
on June 28, 2017)
2. Woon CS : Model Classification and Evaluation of Measurement Uncertainty. J Korea Saf Manag Sci, 9:145-156, 2007.
3. Taverniers I, De Loose M, Van Bockstaele E : Trends in quality in the analytical laboratory. I. Traceability and measurement uncertainty of analytical results. Trends Analyt Chem, 23:480-490, 2004.

4. Squara P, Imhoff M, Cecconi M : Metrology in Medicine: From Measurements to Decision, with Specific Reference to Anesthesia and Intensive Care. Anesth Analg, 120:66-75, 2015.


5. Broadbent BH : A new X-ray technique and its application to orthodontia: the introduction of cephalometric radiography. Angle Orthod, 51:93-114, 1931.
6. Downs WB : Variations in facial relationships: Their significance in treatment and prognosis. Am J Orthod Dentofacial Orthop, 34:812-840, 1948.

7. Chen YJ, Chen SK, Yao JC, Chang HF : The effects of differences in landmark identification on the cephalometric measurements in traditional versus digitized cephalometry. Angle Orthod, 74:155-161, 2004.

8. Baskin H, Cisneros G : A comparison of two computer cephalometric programs. J Clin Orthod, 31:231-233, 1997.

9. Gotfredsen E, Kragskov J, Wenzel A : Development of a system for craniofacial analysis from monitor-displayed digital images. Dentomaxillofac Radiol, 28:123-126, 1999.


10. Yu SH, Nahm DS, Baek SH : Reliability of landmark identification on monitor-displayed lateral cephalometric images. Am J Orthod Dentofacial Orthop, 133:7901-7906, 2008.

11. Power G, Breckon J, Sherriff M, McDonald F : Dolphin Imaging Software: an analysis of the accuracy of cephalometric digitization and orthognathic prediction. Int J Oral Maxillofac Surg, 34:619-626, 2005.


12. Park CY, Park KT : Facemask Effects in Two Types of Intraoral Appliances : Bonded Expander vs. Hyrax. J Korean Acad Pediatr Dent, 42:45-52, 2015.

13. Park SH, Kim YJ, Jang KT, et al. : The Simple Regression Model of Gonial Angles : Comparison between Panoramic Radiographs and Lateral Cephalograms. J Korean Acad Pediatr Dent, 44:129-137, 2017.

15. AlBarakati S, Kula K, Ghoneima A : The reliability and reproducibility of cephalometric measurements: a comparison of conventional and digital methods. Dentomaxillofac Radiol, 41:11-17, 2012.



16. Santoro M, Jarjoura K, Cangialosi TJ : Accuracy of digital and analogue cephalometric measurements assessed with the sandwich technique. Am J Orthod Dentofacial Orthop, 129:345-351, 2006.


17. Farooq MU, Khan MA, Rahman MA, et al. : Assessing the Reliability of Digitalized Cephalometric Analysis in Comparison with Manual Cephalometric Analysis. J Clin Diagn Res, 10:20-23, 2016.

18. Leonardi R, Giordano D, Maiorana F, Spampinato C : Automatic cephalometric analysis: a systematic review. Angle Orthod, 78:145-151, 2008.


20. Ahlqvist J, Eliasson S, Welander U : The effect of projection errors on cephalometric length measurements. Eur J Orthod, 8:141-148, 1986.


21. Hiroshi N, Kenji N, Yoshida Y, Kikuuchi M : Orthodontic diagnosis in bioprogressive therapy. 1st ed. Rocky Mountain Morita Co, 45-54, 1984.
- TOOLS
-
METRICS

-
- 1 Crossref
- 0 Scopus
- 2,952 View
- 290 Download
- Related articles



 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print